
The angle formed at the centre of the circle by lines originating from two points on the circle's circumference is double the angle formed on the circumference of the circle by lines originating from the same points. But x + y is the size of the angle we wanted to find.Ī tangent to a circle is a straight line which touches the circle at only one point (so it does not cross the circle- it just touches it).Ī tangent to a circle forms a right angle with the circle's radius, at the point of contact of the tangent.Īlso, if two tangents are drawn on a circle and they cross, the lengths of the two tangents (from the point where they touch the circle to the point where they cross) will be the same. However, the sum of its angles remains 180°, just like all triangles. They are unequal and its angles are of three different measures. A scalene triangle has sides with varying lengths. A triangle is a closed plane three-sided polygon figure with three sides and three angles. Isosceles (issceles) - un tringulo con 2 lados que tienen. Therefore x + y + x + y = 180, in other words 2(x + y) = 180.Īnd so x + y = 90. In geometry, triangles are defined based on their sides and angles. Isosceles - a triangle with 2 sides having the same length. Since the sum of angles in a triangle 180°. Therefore each of the two triangles is isosceles and has a pair of equal angles.īut all of these angles together must add up to 180°, since they are the angles of the original big triangle. Since QR PR, the angles opposite to them will be equal as well, P Q 36°. We know that each of the lines which is a radius of the circle (the green lines) are the same length. We can construct a bisector for any angle. B StatemenIC Keasom AB BC Given Construct BD as the angle bisector of ZABC, where point Dis on AC.
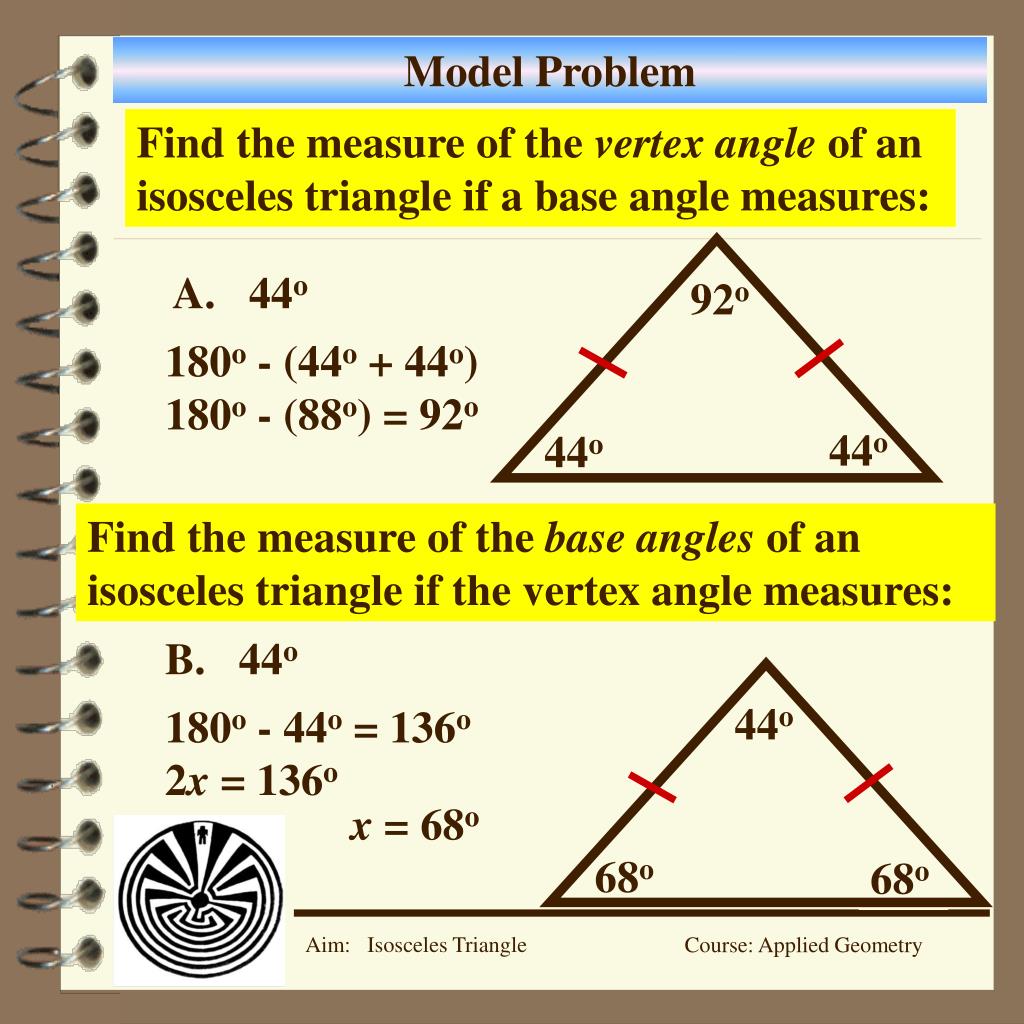
We can split the triangle in two by drawing a line from the centre of the circle to the point on the circumference our triangle touches. Only for this specific isosceles triangle Complete the proof that the base angles of an isosceles triangle are congruent.


 0 kommentar(er)
0 kommentar(er)
